Prime Number란?

Prime Number1

자신보다 작은 두 개의 자연수를 곱하여 만들 수 없는, 1보다 큰 자연수이다.

가장 간단한 방법으로 2 ~ N-1까지 나눠버려 하나라도 나눠떨어지는가를 확인하는 방법이 있다.
이는 한개의 숫자에 대해 소수여부를 판단하는대 O(N)의 시간복잡도를 갖게 된다.
N개의 수의 소수 판단은 O(N^2)의 시간복잡도를 갖게 되므로 이는 실제 알고리즘 문제풀이에서 사용하기 버거운 시간이기에 사용하지 않는다.

이를 해결하기 위한 2가지 소수 판별법 알고리즘이 있다.

방법1: 제곱근

N의 약수는 무조건 sqrt(N)의 범위에 존재한다.

만약 N이 12라 할때, 12의 제곱근은 약 3.46이다.
12의 약수는 1, 2, 3, 4, 6, 12 이다.
여기서 1과 12를 제외했을 때 이는 2 * 6, 3 * 4, 4 * 3, 6 * 2의 결과이다.

이들의 관계는 몫이 커지면 나누는 값이 작아지거나 나누는 값이 커지만 몫이 작아지는 반비례 관계이다. 결국 N의 절반(제곱근)까지 향하게 되면 이후 몫과 나누는 값이 반대로 바뀌게만 되는 상황이다.

따라서 N의 제곱근까지 나누어 떨어지는지 여부를 조사하면 더 빠르게 소수판별을 할 수 있다.

알고리즘

  1. 1은 소수가 아니므로 먼저 처리
  2. 짝수는 소수가 아니므로 false 처리. (단, 2는 짝수이면서 유일한 소수이므로 예외처리 필요)
  3. 2 ~ N제곱근까지 나눠본 후 하나라도 나눠떨어지는 것이 존재하면 false
  4. N제곱근까지 나눴음에도 나눠떨어지지 않는 경우 소수

코드 구현

int isPrime(int n) {
    if( n <= 1 )
        return 0; //1은 소수가 아님.
         
	// 짝수는 소수에서 제외
	// 단, 2는 유일하게 짝수 중에서 소수
    if( n%2 == 0) 
        return n==2 ? 1 : 0;
         
	// n이 홀수인 경우 sqrt(n)까지 나눠서 나눠떨어지는지 여부 체크
    for(int i=3; i<=sqrt(n); i += 2) { 
		// 나눠 떨어진다면 약수에 해당하므로 소수가 아님.
        if( n % i == 0)
            return 0;
    }
    // 위에서 걸러지지 않은 나머지 경우는 소수에 해당됨
	return 1; 
}

시간 복잡도

  • 시간복잡도: O(sqrt(n))

방법2: 에라토스테네스의 체

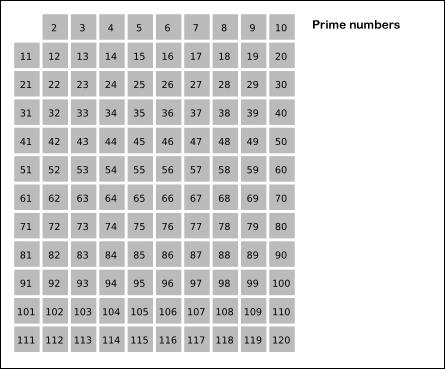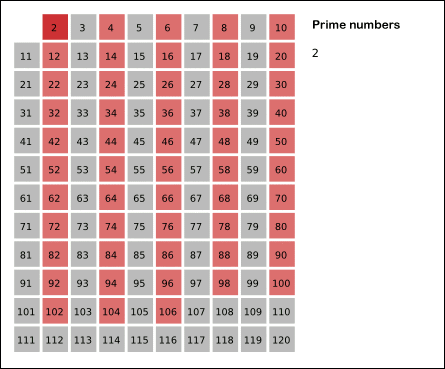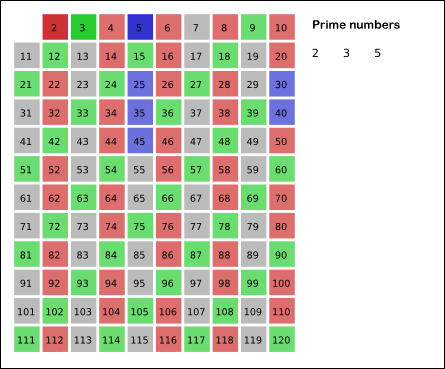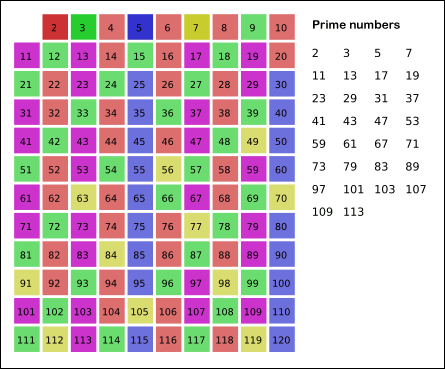
Prime Number2

소수의 배수들을 다 지워나가면 남는 수가 소수이다.

소수(x)의 배수는 약수로 무조건 x를 포함하게 된다.
따라서 절대 소수의 배수는 소수가 될 수 없다. 이를 이용한 것이 에라토스테네스의 체이다.
누구나 알고있는 가장 작은 소수인 2부터 시작해서, 2의 배수를 다 지웠으면, 지워지지 않은 수 중에서 다음 값인 3의 배수를 지워나가고 이를 계속해서 반복해 나가면 소수만 남게된다.
마치 체에 걸러서 남는 것들만 뽑아내는 방식이라고 생각하면 된다.

알고리즘

  1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
  2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
  3. 자기 자신을 제외한 2의 배수를 모두 지운다.
  4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
  5. 자기 자신을 제외한 3의 배수를 모두 지운다.
  6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
  7. 자기 자신을 제외한 5의 배수를 모두 지운다.
  8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
  9. 자기 자신을 제외한 7의 배수를 모두 지운다.
  10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.

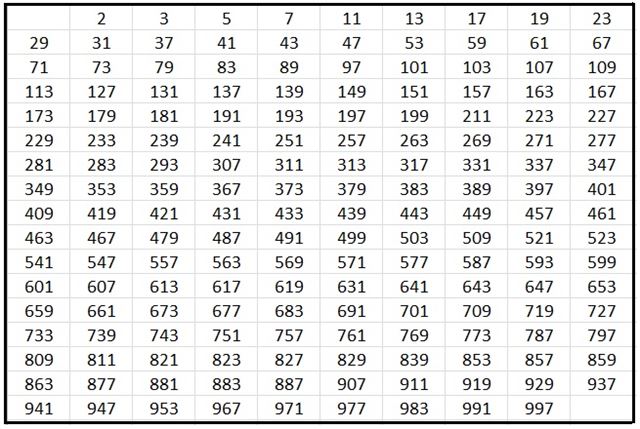
그림의 경우, 11^2 > 120 이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

코드 구현

// 1은 소수가 아니기때문에 따로 처리
int not_prime_nums[MAX_SIZE + 5] = { 0,1,0, };

int isPrime(int n) {

	// 2부터 MAX_SIZE까지 수의 소수 판별
	for (int p = 2; p <= MAX_SIZE; p++) {

		if (not_prime_nums[p] == 0) { // 소수인 경우

			// 소수의 배수는 소수가 아니기때문에 false처리
			for (int i = 2; p*i <= MAX_SIZE; i++)
				not_prime_nums[p*i] = 1;
		}
	
	}
}

시간/공간 복잡도

  • 시간복잡도: O(nloglogn)

참고 자료

관련 문제