Merge Sort(합병정렬)

Merge Sort란?

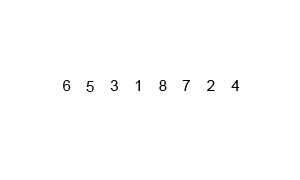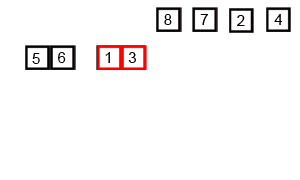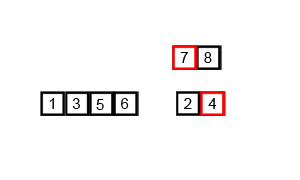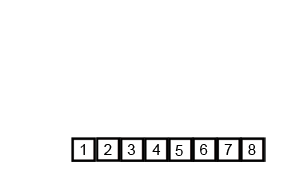
존 폰 노이만에 의해 개발되었으며, 분할정복알고리즘의 하나.
이름 그대로 정렬할 리스트를 쪼개서 작은 단위로 정렬하면서 합쳐나가는 형식으로, 실제로 정렬에 많이 사용되는 방식이다.

방법

위의 리스트를 오름차순으로 정렬할 것이다.

맨 처음에 있던 리스트를 반으로 쪼갠다.

한번 반으로 쪼갠 리스트를 또 반으로 쪼갠다. 쪼갤 수 있는 만큼 계속 쪼갠다.

더이상 쪼갤 수 없는 단계까지 왔다. 이제 합쳐보도록 한다.

합치면서 정렬하는 것이 포인트다. 두 쪼개진 리스트를 비교하며 작은 수를 먼저 넣어간다.

같은 방식으로 두 리스트를 비교하여 작은 값을 먼저 넣어가며 합친다.

완전히 다 합쳐졌다. 의도했던대로 오름차순 정렬이 되었다.

알고리즘

1. 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다.
2. 1번과 같지 않은 경우(리스트의 길이가 2이상)에는 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
3. 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
4. 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.

코드 구현

#include <iostream>
#include <vector>
using namespace std;

vector<int> nums_list; // 정렬할 숫자 리스트

// 합병 부분
void merge(int start, int mid, int end) {
	vector<int> temp;
	
	int md = mid + 1, st = start;

	while (start <= mid && md <= end) {
		nums_list[start] > nums_list[md] ? temp.push_back(nums_list[md++]) : temp.push_back(nums_list[start++]);
	}

	while (start <= mid)
		temp.push_back(nums_list[start++]);
	while (md <= end)
		temp.push_back(nums_list[md++]);

	for (int i = st; i <= end; i++)
		nums_list[i] = temp[i-st];
}

// 리스트 쪼개기 및 병합
void mergeSort(int start, int end) {	
	if (start < end) {
		int mid = (start + end) / 2;

		mergeSort(start, mid);
		mergeSort(mid+1, end);
		merge(start, mid, end);
	}
}

int main() {
	int n;

	scanf("%d", &n);
	nums_list.resize(n);
	
	for (int i = 0; i < n; i++)
		scanf("%d", &nums_list[i]);

	mergeSortSplit(0, n-1);
	
	for (vector<int>::iterator i = nums_list.begin(); i < nums_list.end(); i++)
		printf("%d\n", *i);

	return 0;
}

시간/공간 복잡도

• 최악 시간복잡도: O(nlongn)
• 최선 시간복잡도: O(nlongn)
• 평균 시간복잡도: O(nlongn)
• 공간복잡도: O(n)

참고 자료

• 위키백과